Masters in Engineering (Structured)¶
Programme Content¶
The programme consists of eight 15 credit modules, that will be presented in blocks (each block typically has a duration of one week), and students are to attend these blocks at Stellenbosch University. Online participation of the block week is also possible if students cannot travel to Stellenbosch. No further contact time will be required.
The modules typically consist of 2 weeks pre reading, one lecture week and 6 weeks of post block assignments. Modules offered by other departments can have a different structure/presence requirements.
The five data science modules are compulsory and the student may further select two out of the four generic structured master’s level modules, as well as one specialisation module. Note that additional modules hosted by the Department of Applied Mathematics may be made available as specialisation module options.
For each module, a number of assignments will be completed to test the application of the theory exposed to in the module.
A final 60 credit data science research project must be completed, where the knowledge gained in all eight modules will be applied on a relevant industry related project.
Furthermore, students will automatically be registered for the Professional Communication 871 module of 1 credit to be completed online. Students are also allowed to enrol for the Programming in R (Eng) 774 module for non-degree purposes.
Compulsory Data Science Modules¶
The following data science modules are all compulsory:
| Data Science (Eng) 874 Prof Grobler & Dr Kasongo (Industrial Engineering) |
|---|
| Data science is the application of computational, statistical, and machine learning techniques to gain insight into real world problems. The main focus of this module is on the data science project life cycle, specifically to gain a clear understanding of the five steps in the data science process, namely obtain, scrub/wrangling, explore, model, and interpret. Each of these steps will be studied with the main purpose to gain an understanding of the requirements, complexities, and tools to apply to each of these life cycle steps. Students will understand the process of constructing a data pipeline, from raw data to knowledge. Case studies from the engineering domain will be used to explore each of these steps. |
| Applied Machine Learning 874 Prof Engelbrecht & Mr Burger (Industrial Engineering) |
|---|
| In this module students will be exposed to a wide range of machine learning techniques and gain practical experience in implementing them. Students will not only learn the theoretical underpinnings of several machine learning techniques, gaining an important understanding of the requirements, inductive bias, advantages and disadvantages, but also will gain the practical know-how needed to apply these techniques to real-world problems. The focus will be on information-based learning, similarity-based learning, error-based learning, kernel-based learning, probabilistic learning, ensemble learning, and incremental learning. |
| Optimisation (Eng) 874 Prof Van Vuuren, Dr S Nel (Industrial Engineering) |
|---|
To master the art of building and solving (exactly or approximately) optimisation models of the following types: Linear programming models, assignment, transportation and transhipment models, and integer programming models. Understanding the different classes of optimisation problems and implementing advanced optimisation algorithms to solve real-world optimisation problems. A student who has successfully completed this module will be able to:
|
| Big Data Technologies (Eng) 874 Dr Du Toit (Industrial Engineering) |
|---|
| This module focuses on the tools and platforms for big data management and processing. Big data management refers to the governance, administration and organization of large volumes of data of different types (both structured and unstructured). Efficient platforms to store and manage big data will be considered, including NoSQL, data warehousing, and distributed systems. Big data processing focuses on the 3V-characteristics of big data namely volume, velocity, and variety. Different architectures for big data processing will be studied, including map-reduce and graphical big data models. Students will obtain experience in big data tools and platforms, including Spark, Hadoop, R, and data virtualization. Other aspects of big data, such as data streams, data fusion, and data sources, including social media and sensor data, will be discussed. |
| Data Analytics (Eng) 874 Prof Engelbrecht & Mr Burger (Industrial Engineering) |
|---|
| In this module students will learn the data analytics life cycle, and how to apply each phase of this life cycle to solve engineering data analytics problems. Students will learn techniques for exploratory data analysis, and how to apply machine learning approaches for mining knowledge from data sets, to extract hidden patterns, associations and correlations from data. Students will gain the practical know-how needed to apply data analytics techniques to structured data. Students will learn advanced approaches to data analytics, with a specific focus on visual analytics, image analytics, text analytics, and time series analytics. The student will gain experience in the implementation of various techniques to extract meaning from these different data source types. The advanced data analytics techniques encountered will be applied to data intensive engineering problems. |
Compulsory Generic Structured Master’s Modules¶
Students have to do any two of the following generic faculty master's modules:
| Project Management 873 Dr C Nel (Department of Industrial Engineering) |
|---|
| The module focuses on advanced topics in project management, and it is expected that participants have either attended a project management course or have experience in managing projects. The module builds on the traditional project scheduling by addressing critical chain management and looks at managing project risks through the identification and assessment of risk potentials and mitigating strategies, including resource / cost management and contingency planning. The selection of appropriate teams and structures to facilitate contract management are discussed, along with executing project leadership through proper communication channels. The importance of procurement, from tender procedures through to supplier selection will be highlighted. The different nuances between commercial and research projects will be explained. |
| Advanced Topics in Engineering Management 873 Prof Pistorius & Prof Grobbelaar (Department of Industrial Engineering) |
|---|
| The purpose of the module is to present principles of general management within the context of technical disciplines. The course themes include the business environment and strategic management on a firm level, touching on the role of innovation and technology for competitiveness on a systems level from international and national perspectives. The course will include a significant focus on tools and techniques for technology and innovation management exploring the link between technology management and business management taking a capabilities approach. These capabilities include acquisition, protection, exploitation, identification and selection. We relate traditional approaches to technology management to what it means for the context of the fourth industrial revolution, platform economies and innovation platforms. The functions of engineering management, namely planning, organising, leading and controlling will also be discussed. This will include a specific focus on human resource management, both insofar as managing projects, people and groups is concerned as well as aspects of labour relations and specifically the labour law and contractual requirements in South Africa. We contextualise the above under the theme of “leadership”, with an exploration of different leadership styles, communication and motivation. |
| Numerical Methods TW876 Department of Applied Mathematics |
|---|
| The module focuses on matrix computations. We study the effective solution of linear systems, involving both square and rectangular matrices (least-squares). Direct as well as iterative methods are considered, with the emphasis on sparse matrices and matrices with structure. Numerical methods for the eigenvalue problem are also considered. Pitfalls such as numerical instability and ill-conditioning are pointed out. Model problems are taken from partial differential equations, data analysis and image processing. Theory, algorithmic aspects, and applications are emphasized in equal parts. |
| Project Economics and Finance 812 Department of Civil Engineering |
|---|
| The module focuses on how to finance a business opportunity (project) that can be isolated from the rest of a company’s business activities. Financing through a combination of debt and equity are discussed, based on the future profitability of the project where project cash flow is the main source of capital recovery and the project assets are the only collateral. The concepts of construction loans and public-private partnerships are discussed. A number of case studies will be covered in the module. Module content:
|
Specialisation Modules¶
Any one of the following modules can be selected as the spesialisation module:
| Deep Learning (Industrial Engineering 874) Dr Dufourq (Department of Industrial Engineering) |
|---|
| Many view the advent of deep learning as a revolution that has fundamentally transformed modern machine learning. This module will cover the basics of deep learning. It will start with a recap of neural network fundamentals. The following topics specific to deep learning will then be covered: multi-layer perceptrons, deep feedforward neural networks, convolutional neural networks, various common architectures including AlexNet, GoogLeNet, ResNet, transfer learning, augmentation, Siamese neural networks, image segmentation, interpretability, object detection, autoencoders, recurrent neural networks, text classification and audio classification. |
| Internet of Things (Emerging Topics in Engineering 875) Prof Booysen (Department of Industrial Engineering) |
|---|
| The purpose of the module is to present the principles and application of connected devices in the Internet-of-Things. The module will cover the full stack and value chain, including hardware, communication technologies, system architecture, message brokers, cloud computing, and data storage, data visualisation, and security. The hardware aspects will include sensor technology for the acquisition of measurements, actuators for control, microcontrollers and firmware for decision making and wireless interfaces. Communication technologies will cover wired and wireless communications technologies, including cellular and low-power networks. An overview of brokering and data storage solutions will be covered with an overview of data visualisation. The students will get the opportunity to generate their own data and to use existing data to familiarise themselves with using data science principles in a larger IoT solution. |
| Advanced Design 814 Department of Mechanical and Mechatronic Engineering |
|---|
This course aims to expose students to the solution of optimization problems in engineering. The course will follow a systematic approach to solve optimization problems:
|
| Robotics 814 Department of Mechanical and Mechatronic Engineering |
|---|
| Mathematical modelling of robots; Rigid motions and homogeneous transformations; Forward and inverse kinematics; Denevit-Hartenberg convention; Velocity kinematics: the Jacobian, singularities; Path and trajectory planning; Independent joint control; Robot dynamics: Euler-Lagrange equations, kinetic and potential energy, equations of motion, properties of robot dynamic equations, Newton-Euler formulation; Force control; Computer Vision: camera calibration, image segmentation, vision and servo control. |
| Advanced Dynamics 814 Department of Mechanical and Mechatronic Engineering |
|---|
| Formulate and solve the dynamics of a particle or system of particles: Relative to static or moving axis system; in terms of generalized coordinates and constraints; in terms of virtual displacement and work; in terms of the Lagrange and Hamilton energy principles; for impulsive forces. Formulate and solve the kinematics and dynamics of a rigid body: In terms of rotation kinematics; with the modified Euler rotation equations of motion; for impulsive forces and moments. Prerequisites: Engineering Mathematics 214, Modelling 334, Computer Programming using MATLAB. |
Data Science Research Project and Research Assignment¶
Students will be required to apply and consolidate the knowledge gained throughout this program. For this purpose, students will solve a real-world data science project, providing solutions for each step of the data science project life cycle. As outcome of this project, students will produce a rsearch assignment, describing all of the life cycle phases and research conducted in order to provide a solution to a specific data science problem. It is encouraged that the knowledge gained in specialisation module selected above, is utilised in the project.
Students must have passed their 5 core modules to be allowed to proceed with the data science project.
A call for project proposals will be sent to possible industry and academic partners around mid-year. The project proposals received by the industry and academic partners will then be distributed amongst the students and each student will be required to place a bid for a number of different projects. The industry and academic partners will review the bids and, based on their preferences and the discretion of the programme coordinator, students will be allocated a project.
The company which a student works for will also be allowed to submit a project proposal and specify that the project needs to be completed by a particular student.
Each student will be allocated a supervisor from one of the departments involved in this programme, as well as a mentor from the industry/academic partner if applicable. Upon completion of the project, a research assignment will be completed and submitted for examination by an internal and an external examiner.
Module Co-Requisites¶
A student may choose to enrol for the programme as a full-time or a part-time student, where the main difference is the length of time allowed to enrol. It is expected of a full-time student to complete the programme in two years, however, the student may apply for a 3rd year with good motivation. A part-time student is expected to complete the programme in three years, however, the student may, with good motivation, apply for extension. Note that a change from full time study to part time study is not possible once you begin the programme.
In considering the part-time option, it is critical for the student to consider the co-requisites of modules, meaning that the student must have previously been registered for the co-requisite module or be registered for it in parallel, irrespective of the performance in the module. The module co-requisites are as follows:
| Modules | Co-requisite Modules |
|---|---|
| Applied Machine Learning 874 | Data Science (Eng) 874 |
| Optimisation (Eng) 874 | Data Science (Eng) 874, Applied Machine Learning 874 |
| Big Data Technologies (Eng) 874 | Data Science (Eng) 874, Applied Machine Learning 874, Optimisation (Eng) 874 |
| Data Analytics (Eng) 874 | Data Science (Eng) 874, Applied Machine Learning 874, Optimisation (Eng) 874 |
| Deep Learning (Industrial Engineering 874) | Data Science (Eng) 874, Applied Machine Learning 874 |
All the data science modules are prerequisites to the project and should therefore have been completed before the student can register for the project module.
Admission Requirements¶
To be considered for admission you must:
- Hold at least a BEng, a BScHons, another relevant four-year bachelor’s degree, an MTech, a BTechEng(Hons), or a PGDip (Eng); or
- Hold other academic degree qualifications and appropriate experience that have been approved by the Faculty Board. The department’s chairperson must make a recommendation regarding such a qualification and experience to the Faculty Board.
Students must have passed 1st year
- Mathematics, Statistics or Applied Mathematics; and
- Computer programming (proof of any assessed programming qualification will also be considered).
Note that the marks of your last academic degree will be evaluated against an annual minimum requirement, as this is a competitive programme.
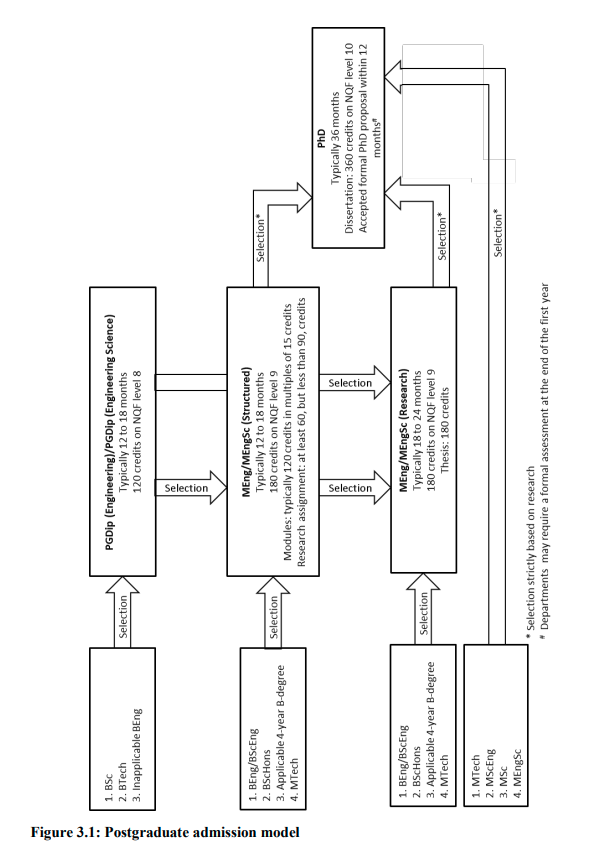
Also refer to the postgraduate admission model in Figure 3.1, in Section 3.2 in the Engineering Calendar, reproduced below: